Off Policy Train을 통해, Sample Efficiency를 높여보자.

Soft Actor Critic 분석

  • Soft Actor Critic은 Policy Gradient 방식인 Actor Critic 모델의 변형이면서도 Replay Buffer로 train하는 off policy 모델이다. PG이면서도 off policy가 가능한 것은 Soft Q-Learning을 기반으로 하기 때문이다.
  • SAC는 Continuous Action Space를 대상으로 하는 모델이다. SAC를 Discrete Action Space에 적용할 수 있도록 수정한 모델도 있다.
  • 논문에서는 4족보행로봇(locomotion for a quadrupedal robot)에서 SOTA 성능이 나온다고 언급하고 있다. 전반적인 task에서는 PPO보다 못하다.

개요

PPO SAC

*그림: PPO가 SAC보다 안정적이다. SAC모델 결과가 좀 더 불안정해 보이는 이유는, SAC 모델이 가능한 random action을 추구하면서도 임무(task)를 성공시키는 것이 목적이기 때문이다.

Policy & Entropy

  • Policy Gradient의 일반적인 이야기를 해보자. Policy Gradient의 Objective Function은 다음과 같은 형태로 주어진다. 확률 \(p\)인 action을 취해 reward \(r\)을 받은 상황이다.

\(\max\ [r\log p] \quad \quad \text{or} \quad \quad \max\ [A \log p]\)

  • Policy 최적화는 높은 reward \(r\)을 주는 확룰 \(p\)를 더 크게 하거나 높은 advantage \(A\)를 주는 확률 \(p\)를 더 크게 하려고 최적화를 수행한다. (\(r,p\))의 쌍이 묶여 있기 때문에 on policy가 된다. gradient update(train)을 통해 network이 변했다면, network이 생성하는 새로운 확률은 reward \(r\)을 만들어낸 확률이 아니다. 이러한 이유로 off policy가 될 수 없다.

  • SAC에서는 Objective Function이 다음과 같이 주어진다.
\[\max\ \big[Q + \alpha (-\log p)\big] \quad \quad \text{or} \quad \quad \min\ \big[\alpha \log p - Q\big]\]
  • 이 식은 2가지로 해석할 수 있다.
    • 해석1: target 확률을 \(\frac{1}{\alpha}\exp(Q)\)(또는 softmax \(Q\))로 보고, 확률 \(p\)를 생성한 distribution \(\pi\)와 \(\frac{1}{\alpha}\exp Q\)와의 KL-Divergence를 최소화 한다. 즉 \(D_{KL}\big(\pi \ \Vert\ \frac{1}{\alpha}\exp Q\big) \approx \alpha \log p - Q\)
    • 해석2: \(Q\)값과 entorpy \((-\log p)\)의 weighted sum을 최대화한다. entropy의 weight가 \(\alpha\)이다. \(Q\)를 advantage로 대체하는 것도 가능하다.
  • SAC는 보통의 Policy Gradient와 다른 Soft Q-Learning을 사용하기 때문에, Replay Buffer를 사용하는 Off Policy 모델이다. Soft Q-Learning은 \(\exp Q\) (또는 softmax \(Q\)) 값을 policy 확률로 보는 방법이다.

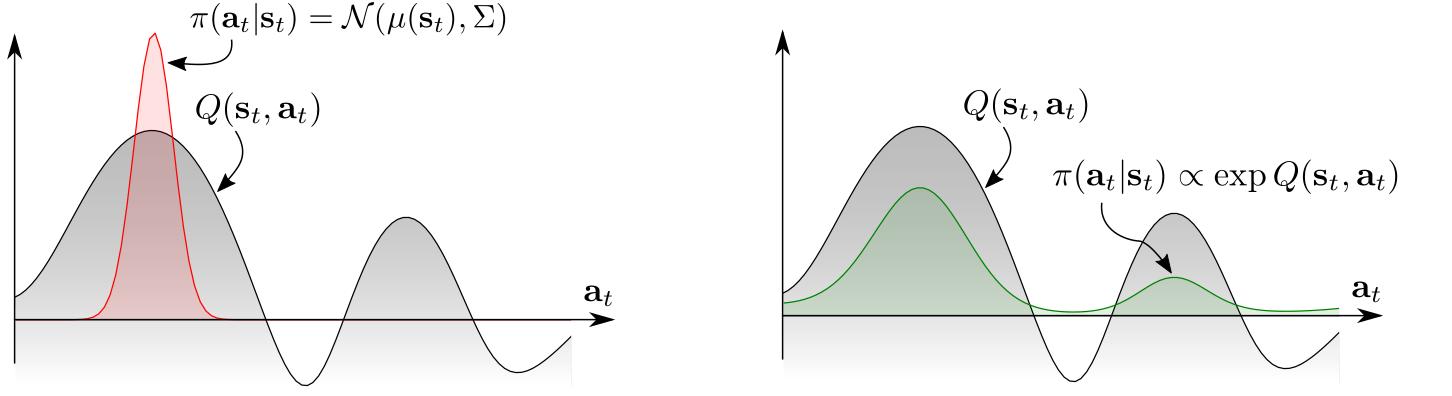
*그림: A multimodal \(Q\)-function: 1. 왼쪽 그림과 같은 \(Q\)-function이 주어져 있을 때, policy를 정규분포로 예측한다면, 오른쪽의 작은 mode에 대한 action 확률이 높아질 수 없다. 2. policy를 \(\exp Q(s_t,a_t)\)에 비례하게 만든다면, 상황 변화에 더 잘 대응할 수 있는 모델을 만들 수 있다.

  • SAC모델은 일반적인 sate value function을 대신하여, soft state value function을 다음과 같이 정의한다. 일반적인 state value function에 etropy term을 추가하여 exploration이 가능하도록 했다.
\[\begin{eqnarray} H(p) &=& \mathbb{E}_{x\sim p} \Big[ -\log p(x) \Big], \nonumber\\ V(s_t) &=& \mathbb{E}_{a_t\sim\pi} \big[ Q(s_t,a_t) \big] +\alpha H \big(\pi(\cdot | s_t)\big) \nonumber\\ &=& \mathbb{E}_{a_t\sim\pi} \big[ Q(s_t,a_t) -\alpha \log \pi(a_t \vert s_t) \big] \ \ \text{for } \alpha > 0, \label{eq43}\tag{1}\\ Q(s_t,a_t) &=& \mathbb{E}_{s_{t+1}\sim p, a_{t+1} \sim \pi} \Bigg[ r(s_t, a_t, s_{t+1}) + \gamma \Big( Q(s_{t+1}, a_{t+1}) + \alpha H(\pi(\cdot | s_{t+1})) \Big) \Bigg]\nonumber \\ &=& \mathbb{E}_{s_{t+1}\sim p} \Bigg[ r(s_t, a_t, s_{t+1}) + \gamma V(s_{t+1}) \Bigg] \nonumber \end{eqnarray}\]
  • entropy regularization coefficient(or temperature coefficient) \(\alpha\)는 상수로 고정하는 경우도 있고, training을 통해 update하는 경우도 있다.

  • 이론적으로 위와 같이 soft value function을 정의해도 optimal policy로 수렴한다.

  • Policy Network(\(\pi_\phi\)), Value Network(\(V_\psi, V_{\bar{\psi}}\)), Q-Network(\(Q_{\theta}\))이 필요하다. Value값은 \(Q\)값으로 부터 구할 수도 있지만, SAC에서는 모델의 안정성을 위해 별도의 Value Network을 두었다. \(V_{\bar{\psi}}\)는 Value target Network으로 train 대상이 되지는 않고, \(V_\psi\)로 부터 exponentially moving average로 update된다. 두번째 SAC 논문에서는 Value Network 없이 Q-Network만으로 구현하고 있다. continuous action space이기 때문에, Q-Network의 입력은 state와 action의 concat이 된다.
  • SAC는 Replay Buffer를 사용하는 off policy 모델이다. Replay Buffer \(\mathcal{D} = \{ (s_t,a_t,r_t,d_n,s_{t+1}) \}\)로 구성된다.
  • Value Loss: Value Network \(V_\psi\) training.
\[\begin{eqnarray} J_V(\psi) = \mathbb{E}_{s_t \sim \mathcal{D}}\Bigg[{\frac{1}{2}\bigg(V_\psi(s_t) - \mathbb{E}_{\bar{a}_t\sim\pi_\phi}\big[{Q_\theta(s_t, \bar{a}_t) - \alpha\log \pi_\phi(\bar{a}_t|s_t)}\big] \bigg)^2} \Bigg] \label{eq41}\tag{2} \end{eqnarray}\]

*그림: Value Loss: \(\bar{a}_t\)는 replay buffer에서의 action이 아니고, policy network에서 새롭게 생성한 action이다. 참고로 \(s_t\) 대신 \(s_{t+1}\)를 이용해서 value loss를 구할 수도 있다.

  • 식(\(\ref{eq41}\))에서 기대값을 직접 계산하기 어렵기 때문에 policy network \(\pi_\phi\)에서 sampling을 통해 action \(\bar{a}_t\)를 뽑아서 계산하면 된다.
\[\mathbb{E}_{\bar{a}_t\sim\pi_\phi}\big[Q_\theta(s_t, \bar{a}_t) - \alpha\log \pi_\phi(\bar{a}_t|s_t)\big] \ \rightarrow \ Q_\theta(s_t, \bar{a}_t) - \alpha\log \pi_\phi(\bar{a}_t|s_t)\]

  • Q-Function Loss: Q-Network(\(Q_{\theta}\)) training. \(\begin{eqnarray} J_Q(\theta) &=& \mathbb{E}_{(s_t,a_t)\sim\mathcal{D}} \Bigg[ \frac{1}{2} \bigg( Q_\theta(s_t,a_t) - \underbrace{\hat{Q}(s_t,a_t)}_{\text{stop gradient}} \bigg)^2 \Bigg] \ \ \text{with} \nonumber \\ \hat{Q}(s_t,a_t) &:=& r(s_t,a_t) + \gamma \mathbb{E}_{s_{t+1}\sim p} \Big [ V_{\bar{\psi}} (s_{t+1}) \Big] \ \ \leftarrow {p: \text{transition probability.}} \label{eq42}\tag{3} \end{eqnarray}\)

  • next state \(s_{t+1}\)은 \(s_{t+1}\sim p\)로 표시되어 있지만, 구현에서는 replay buffer에 있는 \(s_{t+1}\)이다. \(\hat{Q}(s_t,a_t)\)의 gradient는 계산되지 않아야 한다.
  • 식(\(\ref{eq41}\))에서 Value Network의 target에 Q-Network값이 사용되고, 식(\ref{eq42})에서 Q-Newtork의 target에 Value Network이 사용된다. 이런 순환 참조 구조를 벗어나기 위해, Value Network의 copy인 Value target Network \(V_{\bar{\psi}}\)를 만드는 것이다. 또 다른 측면으로, 식(\ref{eq42})에서 Value Network \(V_{\psi}\) 대신 target Network \(V_{\bar{\psi}}\)를 사용하는 것은 DQN에서 main network, target network으로 2개 사용하는 것과 같은 원리이다.
  • target value Network \(V_{\bar{\psi}}\) update 시키는 방식 2가지.
    • 주기적으로(periodically) update.
    • Polyak averaging: exponentially weighted averaging
  • Policy Loss: expected KL-Divergence
\[J_{\pi}(\phi) = \mathbb{E}_{s_t \sim \mathcal{D}} \Bigg [ D_{KL} \bigg( \pi_{\phi} (\cdot | s_t)\ \Vert\ \frac{\exp(\frac{1}{\alpha}Q_\theta(s_t, \cdot))}{Z_\theta(s_t)} \bigg) \Bigg]\]
  • 보통의 Policy Gradient 모델이 Off Policy 방법을 적용하기 위해, Old Policy로 생성된 Reaplay Buffer의 data로 New Policy를 update하기 위한 방법이 있어야 한다. TRPO, PPO에서는 probability ratio를 이용한 important sampling 기법을 사용한다. SAC에서는 \(\exp Q(s_t,\cdot)\)를 normalization(\(Z_\theta(s_t)\))해서 확률분포로 간주한다. 그래서 new policy와 \(\exp Q(s_t, \cdot)\)의 KL-Divergence가 최소화 되도록 한다. 실제 계산에서는 normalization term인 \(Z_\theta(s_t)\)는 무시해도 된다.
\[\begin{eqnarray} J_{\pi}(\phi) &=& \mathbb{E}_{s_t \sim \mathcal{D}} \Bigg [ \mathbb{E}_{\bar{a}_t\sim \pi_{\phi}} \Big[ \alpha \log \pi_{\phi} ( \bar{a}_t | s_t) - Q_\theta(s_t, \bar{a}_t) \Big] \Bigg] \label{eq44}\tag{4} \\ &\approx& \mathbb{E}_{s_t \sim \mathcal{D}} \Big [ \alpha \log \pi_{\phi} ( \bar{a}_t | s_t) - Q_\theta(s_t, \bar{a}_t) \Big] \label{eq49} \tag{5} \end{eqnarray}\]
  • 이 식에서도 기대값 계산은 Value Loss와 동일하게 sampling을 통해 처리한다. 그런데, sampling된 \(\bar{a}_t\)에 관한 backpropagation의 미분이 필요하기 때문에 Policy Network의 distribution에서 reparameterization trick이 필요하다.
  • 식(\ref{eq43}), (\ref{eq44})를 비교해 보자. KL-Divergence를 최소화 한다는 것과 soft value function 값을 최대화 한다는 것이 동치라는 것을 알 수 있다.
  • 2개의 \(Q\)-Networks: Our algorithm also makes use of two Q-functions to mitigate positive bias in the policy improvement step that is known to degrade performance of value based methods. \(Q_{\theta}\) 대신, 2개의 \(Q_{\theta_1}, Q_{\theta_2}\)을 각각 독립적으로 train 시켜서 min값을 적용한다. 이런 방법은 train 속도 향상에도 도움이 된다. 식(\ref{eq41}), (\ref{eq44})에서 \(Q_\theta\)를 \(\min \big[ Q_{\theta_1}, Q_{\theta_2} \big]\)으로 바꾸면 된다.
  • squashing function \(\tanh\): 보통 continuous action space에서 policy network은 정규분포로 모델링하고 action range를 벗어나는 action은 clipping으로 처리한다. SAC논문에서는 \(u\sim N(\mu,\sigma)\)를 예측하고 \(a=\tanh(u)\)로 action을 예측했다. 따라서 action \(a\)의 likelihood(probability density function(pdf)값)은 change of variables를 이용해서 계산해주면 된다.
  • 먼저 일반적인 확률 변수와 확률밀도 함수에서의 change of variables에 대해 살펴보자. 확률 변수 \(X\)의 pdf가 \(f_X(x)\)라 하자. 이때 확률변수 \(Y:=g(X)\)의 pdf를 구하는 과정이 change of variables이다. 확률 변수 \(Y\)의 pdf \(f_Y(y)\)는 다음과 같이 주어진다.
\[\begin{eqnarray*} f_Y(y) &=& f_X\big(g^{-1}(y)\big) \overbrace{\left| \frac{d}{dy} g^{-1}(y) \right|}^{\text{Jacobian determinant의 절대값}} \\ &=& f_X(x) \left| \frac{d}{dy} g^{-1}(y) \right| \end{eqnarray*}\]
  • \(u\)의 pdf를 \(\mu(u\vert s)\)라 하자. 우리의 경우는 \(u=\tanh^{-1}(a)\)의 jacobian(\(\frac{du}{da}\))이 대각행렬이기 때문에, \(\tanh\)의 역함수를 미분해야 하는 \(\frac{du}{da}\)보다는 \(\tanh\)를 바로 미분하는 \(\frac{da}{du}\) 미분해서 역수를 취하는 것이 낫다.
\[\begin{eqnarray*} \frac{da}{du} &=& \text{diag}(1-\tanh^2(u)) \\ \pi(a\vert s) &=& \mu(u\vert s) \left| \det\left( \frac{du}{da} \right) \right| \\ &=& \mu(u\vert s) \left| \det\left( \frac{da}{du} \right) \right|^{-1} \\ \log \pi(a\vert s) &=& \log \mu(u\vert s) - \sum_i \log \big( 1-\tanh^2(u_i) \big) \end{eqnarray*}\]
  • 여기서 \(\mu(u\vert s)\)의 각 action 성분이 uncorrelated되어 있다면, 확률은 각 action 성분 확률의 곱이 된다. 따러서,
\[\log \mu(u\vert s) = \sum _i \log \mu(u_i \vert s)\]

두번째 논문: Value Network 없이 Q-Network만으로 모델 구성

  • Value Network없이 Q-Network과 Policy Network으로만 구성. Q-Network이 \(Q_{\theta_1}, Q_{\theta_2}\) 2개 있어야 하고, target Q-Network \(Q_{\bar{\theta}_1}, Q_{\bar{\theta}_2}\)도 있어야 하기 때문에, 모두 4개의 Q-Network이 필요하다.
  • Value Network이 사용되는 식(\ref{eq42})를 수정해야 한다. Replay Buffer \(\mathcal{D}\)로 부터 data \((s_t,a_t,r_t,d_n,s_{t+1})\)가 주어져 있다면, Policy Network에 \(s_{t+1}\)을 넣어 sampling하면 \(\bar{a}_{t+1}, \pi(\bar{a}_{t+1} \vert s_{t+1})\)를 얻을 수 있다.
\[\begin{eqnarray} J_Q(\theta_i) &=& \mathbb{E}_{(s_t,a_t)\sim\mathcal{D}} \Bigg[ \frac{1}{2} \bigg( Q_{\theta_i}(s_t,a_t) - \underbrace{\hat{Q}(s_t,a_t)}_{\text{stop gradient}} \bigg)^2 \Bigg] \ \ \text{with} \nonumber \\ \hat{\mathbb{Q}}(s_t,a_t) &=& r(s_t,a_t) + \gamma \mathbb{E}_{a_{t+1}\sim p}\Bigg(\min\Big [ Q_{\bar{\theta}_1}(s_{t+1},a_{t+1} ), Q_{\bar{\theta}_2}(s_{t+1},a_{t+1} ) \Big] - \alpha \log \pi(a_{t+1} \vert s_{t+1}) \Bigg) \label{eq45}\tag{6}\\ &\approx& r(s_t,a_t) + \gamma \Bigg(\min\Big [ Q_{\bar{\theta}_1}(s_{t+1},\bar{a}_{t+1} ), Q_{\bar{\theta}_2}(s_{t+1},\bar{a}_{t+1} ) \Big] - \alpha \log \pi(\bar{a}_{t+1} \vert s_{t+1}) \Bigg) \label{eq46}\tag{7} \end{eqnarray}\]
  • 식(\ref{eq45})와 같이 state \(s_{t+1}\)에서의 기대값을 계산해야 하지만, 기대값을 계산하기 어려우므로 대신 특정 action \(\bar{a}_{t+1}\)을 하나 생성해서 식(\ref{eq46})과 같이 처리한다. 만약 discrete action space였다면, 그 기대값을 계산하기가 쉽다.

Temperature Hyperparameter \(\alpha\) Train Model

  • entropy regularization coefficient(or temperature coefficient) \(\alpha\)를 hyperparameter로 고정하지 않고, train을 통해 찾는 방법을 생각해 보자. minimum policy entropy threshold인 상수 \(\mathcal{H}_0\)에 대하여, entropy가 \(\mathcal{H}_0\)보다 커지도록 제약을 둔다고해보자
\[\begin{eqnarray*} & &\max_{\pi_0, \dots, \pi_T} \mathbb{E} \Bigg[ \sum_{t=0}^T r(s_t, a_t)\Bigg] \\ \text{s.t. } & & \mathbb{E}\Big[-\log \pi_t(a_t|s_t) \Big] \geq \mathcal{H}_0, \ \ \forall t \end{eqnarray*}\]
  • 이 문제를 dual problem으로 변환 후, time step \(t=T, T-1, T-2, \cdots\) 순서의 backward로 전개하여 최종적인 minimization 문제의 objective function을 얻게 된다.
\[\begin{eqnarray} J(\alpha) &=& \mathbb{E}_{a_t\sim \pi_t} \Big[ -\alpha \log \pi_t(a_t \vert s_t) - \alpha \mathcal{H}_0 \Big] \label{eq47}\tag{8}\\ &=& \alpha \overbrace{\mathbb{E}_{a_t\sim \pi_t} \Big[ - \log \pi_t(a_t \vert s_t) - \mathcal{H}_0 \Big]}^{\text{stop gradient}}\\ &\approx& -\alpha \log \pi_t(\bar{a}_t \vert s_t) - \alpha \mathcal{H}_0 \label{eq48}\tag{9} \end{eqnarray}\]
  • 자세한 전개 과정은 이곳을 참고하면 된다. dual problem으로 변환해서 전개한 후, 실질적으로 \(\alpha\)를 구하는 network과 policy를 구하는 network이 분리되어 구해져야 하기 때문에, \(Q_t, \pi_t\)를 구한 후, \(\alpha_t\)를 구하게 된다. 그래서 \(Q, \pi\)와 분리된 \(\alpha\)만의 optimization 문제가 만들어진다. 즉 \(J(\alpha)\)를 최소화 하면 된다. \(J(\alpha)\)도 기대값으로 표현된 식인데, 구체적인 기대값을 구하기 어렵기 때문에, 식(\ref{eq46})와 같은 방식으로 Policy Network에 \(s_t\)를 넣어 action \(\bar{a}_t\)를 하나 sampling해서 식(\ref{eq48})과 같이 대체할 수 있다.
  • 이 식의 직관적인 의미는 단순하다.
    • entropy \(-\log \pi_t(a_t \vert s_t)\)가 \(\mathcal{H}_0\)보다 크면, minimization을 위해서 \(\alpha\)값을 줄이게 된다. 즉 entropy가 너무 크면 식(\ref{eq43}), (\ref{eq44})에서 \(\alpha\)값을 0에 가깝게 만든다.
    • 반대로, entropy가 \(\mathcal{H}_0\)보다 작으면, \(\alpha\)값이 커지게 된다.
    • 구현에서는 target entropy \(\mathcal{H}_0\)를 0보다 낮게 잡아놓고, \(\alpha\)값이 train을 할 수록 계속 낮아지게 한다. \(\alpha\)의 초기값과 leaning rate을 잘 설정해야 한다.
  • 참고로 \(t=T\)인 경우에 대해서만, dual problem을 살펴보자. dual variable \(\alpha_T \geq 0, -\log\pi_T(a_T \vert s_T) \geq \mathcal{H}_0\)에 대하여 다음 식이 성립한다.
\[A_T: = \max_{\pi_T} \mathbb{E}_{s_T, a_T} \Big [ r(s_T, a_T) \Big] \leq \max _{\pi_T} \mathbb{E} \Big[ r(s_T, a_T) + \alpha_T\big( -\log\pi_T(a_T \vert s_T) - \mathcal{H}_0 \big) \Big] \ \longleftarrow \text{constraint 조건 하에서}\]
  • 여기서 constraint \(-\log\pi_T(a_T \vert s_T) \geq \mathcal{H}_0\) 조건을 제거(\(\alpha_T \geq 0\)은 유지)하면 더 다양한 값을 가질 수 있으므로 max값이 더 커질 수 있다. 따라서, 다음 식이 성립한다(weak duality).
\[\overbrace{A_T}^{\text{constraint가 적용된 최대값}} \leq \quad \quad \max _{\pi_T} \mathbb{E} \Big[ r(s_T, a_T) + \alpha_T\big( -\log\pi_T(a_T \vert s_T) - \mathcal{H}_0 \big) \Big]\]
  • 이 식은 모든 \(\alpha_T \geq 0\)에 대하여 성립하므로, minimum을 취해도 성립한다.
\[A_T \quad \leq \quad \min_{\alpha_T \geq 0} \max _{\pi_T} \mathbb{E} \Big[ r(s_T, a_T) + \alpha_T\big( -\log\pi_T(a_T \vert s_T) - \mathcal{H}_0 \big) \Big]\]
  • 그런데 이 부등식은 등식으로 성립한다. 이유는 Slater’s condition이 만족되어, strong duality가 성립하기 때문이다(the objective is linear and the constraint (entropy) is convex function in \(\pi_T\)).
\[A_T = \min_{\alpha_T \geq 0} \max _{\pi_T} \mathbb{E} \Big[ r(s_T, a_T) + \alpha_T\big( -\log\pi_T(a_T \vert s_T) - \mathcal{H}_0 \big) \Big]\]
  • 이 식을 직관적으로 이해해 볼 수 있다. constraint 즉 \(-\log\pi_T(a_T \vert s_T) \geq \mathcal{H}_0\) 가 만족되지 않으면, 양수 \(\alpha_T\)를 무한히 키워서 전체 값이 \(-\infty\)로 가게 되는데, 이렇게 해서는 원하는 최대화가 되지 않는다. 따라서, 최대화를 이루기 위해서는 constraint가 만족될 수 밖에 없다.

Soft Actor Critic with Discrete Action Space

  • Discrete Action Space에서는 sampling을 통해 근사적으로 기대값을 계산하지 않고, 기대값을 직접 계산할 수 있다. 식(\ref{eq49}), (\ref{eq46}), (\ref{eq48})을 원래대로 식(\ref{eq44}), (\ref{eq45}), (\ref{eq47})로 계산할 수 있다. 따라서, sampling이 필요없고, replay buffer에 있는 data만 사용하면 된다.
  • Discrete Soft Actor Critic 구현은 DQN 구현과 유사한 측면이 많다.
  Policy Network main Q-Network target Q-Network  
Policy Loss \(\pi_\phi(s_t)\) \(Q_{\theta_i}(s_t)\)   식(\ref{eq44})
\(Q\)-Loss \(\pi_\phi(s_{t+1})\) \(Q_{\theta_i}(s_t,a_t)\) \(\leftarrow\) prediction \(Q_{\bar{\theta}_i}(s_{t+1})\) 식(\ref{eq45})
\(\alpha\)-Loss \(\pi_\phi(s_t)\)     식(\ref{eq47})

표: Discrete Soft Actor Critic: Ploicy Network의 Policy Loss, \(Q\)-Loss를 계산할 때는 tensorflow graph의 reuse가 필요하다. main \(Q\)-Network은 \(Q_{\theta_i}(s_t)\)를 한번 계산한 후, \(Q\)-Loss에서는 \(a_t\)에서의 값만 indexing하면 된다.

Gym Games

  • Discrete Action, CartPole-v1: vanilla Policy Gradient 정도의 성능이 나온다.
  • Continous Action, Pendulum-v0: PPO보다 train 속도가 느리고, 결과도 좀 불안정하다. 이유는 위의 gif 그림을 참고하면 된다.
  • BreakoutDeterministic-v4: train이 잘 되지 않는다.
  • BipedalWalker-v3: train 속도는 PPO보다 느리다. SAC로 train한 모델이 더 빨리 나아간다.
PPO SAC

Reference